Для каждого числа а¹0 существует обратное число а^-1 такое, что произведение а×а^-1=1. Для квадратных матриц вводится аналогичное понятие.

Определение.Если существуют квадратные матрицы Х и А одного порядка, удовлетворяющие условию:

XA = AX = E,

где Е — единичная матрица того же самого порядка, что и матрица А, то матрица Х называется обратнойк матрице А и обозначается А^-1.

Из определения следует, что только квадратная матрица имеет обратную; в этом случае и обратная матрица является квадратной того же порядка.

Однако, не каждая квадратная матрица имеет обратную. Если условие а¹0 является необходимым и достаточным для существования числа а^-1, то для существования матрицы А^-1 таким условием является требование DA¹0.

Определение. Квадратная матрица n-го порядка называется невырожденной (неособенной), если ее определитель DA¹0.

Если же DA=0, то матрица А называется вырожденной (особенной).

Теорема (необходимое и достаточное условие существования обратной матрицы). Если квадратная матрица неособенная (т.е. ее определитель не равен нулю), то для нее существует единственная обратная матрица.

Доказательство.

I. Необходимость. Пусть матрица А имеет обратную А^-1, т.е. АА^-1= А^-1А=Е. По свойству 3 определителей (§11) имеем D(АА^-1)= D(А^-1) D(А)= D(Е)=1, т.е. DA¹0 и DA^-1¹0.

I I. Достаточность. Пусть квадратная матрица А неособенная, т.е. DA¹0. Напишем транспонированную матрицу А^Т:

А^Т = .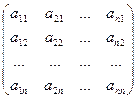

В этой матрице каждый элемент заменим его алгебраическим дополнением, получим матрицу:

А^* = .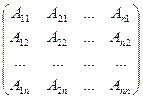

Матрица А^* называется присоединенной матрицей к матрице А.

Найдем произведение АА^* (и А^*А):

АА^* = ,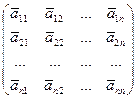

Где диагональные элементы 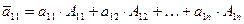= DA,

=DA,

:

:

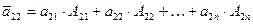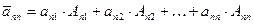=DA.(формуле 11.1 §11)

А все остальные недиагональные элементы матрицы АА^* равны нулю по свойству 10 §11,например:

,

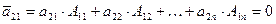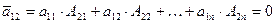и т.д. Следовательно,

АА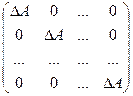^* = или АА^* = DA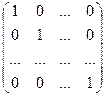= DA×Е.

Аналогично доказывается, что А^*А = DA×Е.

Разделив оба полученных равенства на DA, получим: 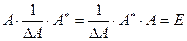. Отсюда, по определению обратной матрицы, следует существование обратной матрицы

 

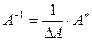, т.к. АА^-1=А^-1А=Е.

 

Существование обратной матрицы доказано. Докажем единственность. Предположим, что существует еще другая обратная матрица F для матрицы А, тогда AF = E и FA = E. Умножив обе части первого равенства на А^-1 слева, а второго на А^-1 справа, получим: А^-1AF = А^-1E и FA А^-1 = E А^-1, откуда EF = А^-1E и FE = E А^-1. Следовательно, F = А^-1. Единственность доказана.

Пример. Дана матрица А = 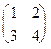, найти А^-1.

 

 

Алгоритм вычисления обратной матрицы:

1. Находим определитель исходной матрицы. Если DA =0, то матрица А-вырожденная и обратная матрица А^-1 не существует. Если DA ¹0, то матрица А-невырожденная и обратная матрица А^-1 существует.
2. Находим алгебраические дополнения элементов исходной матрицы А_ij и составляем из них присоединенную матрицу А^*, записывая алгебраические дополнения элементов строки в столбец.
3. Вычисляем обратную матрицу по формуле: .
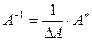4. Проверить правильность вычисления обратной матрицы

Свойства обратных матриц.

1) (A^-1)^-1 = A;

2) (AB)^-1 = B^-1A^-1

3) (A^T)^-1 = (A^-1)^T.

 

 

Простейшие матричные уравнения

⇐ ПредыдущаяСтр 3 из 4Следующая ⇒

 

Рассмотрим матрицы

; ;

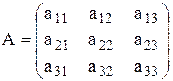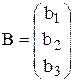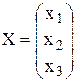
Причем элементы матриц А и В заданы, а Х₁, Х₂, Х₃ – неизвестные.

Тогда уравнение А × Х = В называется простейшим матричным уравнением.

Чтобы его решить, т.е. найти элементы матрицы неизвестных Х, поступим следующим образом:

1. Умножим обе части уравнения на матрицу А^-1, обратную для матрицы А, слева:

А^-1 (А × Х) = А^-1 × В

2. Используя свойство умножения матриц, запишем

(А^-1 × А) Х = А^-1 × В

3. Из определения обратной матрицы

(А^-1 × А = Е) имеем Е × Х = А^-1 × В.

4. Используя свойство единичной матрицы (Е × Х = Х), окончательно получим Х = А^-1 × В

Замечание. Если матричное уравнение имеет вид Х × С = Д, то для нахождения неизвестной матрицы Х уравнение необходимо умножать на С^-1справа.

Пример. Решить матричное уравнение

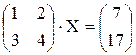
Решение. Введем обозначения

А = 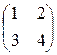; В = ,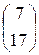

Их определения умножения матриц с учетом размерностей А и В матрица неизвестных Х будет иметь вид

Х =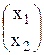

С учетом введенных обозначений имеем

А × Х = В откуда Х = А^-1 × В

Найдем А^-1 по алгоритму построения обратной матрицы

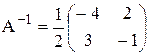
Вычислим произведение

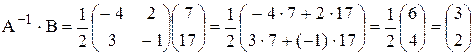
Тогда для Х получим

Х = 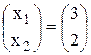откуда х₁ = 3, х₂ = 2

 

Ранг матрицы

 

Рассмотрим матрицу А размера (m x n)

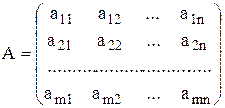
Минором к-ого порядка матрицы А будем называть определитель порядка к, элементами которого являются элементы матрицы А, стоящие на пересечении любых К строк и любых К столбцов. Очевидно, к £ min (m, n).

Определение. Рангом r(A) матрицы А называется наибольший порядок минора этой матрицы, отличного от нуля.

Определение. Всякий отличный от нуля минор матрицы, порядок которого равен ее рангу, называется базисным минором.

Определение. Матрицы, имеющие одинаковые ранги, называются эквивалентными.

 

Вычисление ранга матрицы

 

Определение. Матрица называется ступенчатой, если под первым ненулевым элементом каждой ее строки стоят нули в нижележащих строках.

Теорема. Ранг ступенчатой матрицы равен числу ее ненулевых строк.

Таким образом, преобразуя матрицу к ступенчатому виду, несложно определить ее ранг. Эта операция осуществляется с помощью элементарных преобразований матрицы, которые не изменяют ее ранга:

— умножение всех элементов ряда матрицы на число l ¹ 0;

— замена строк столбцами и наоборот;

— перестановка местами параллельных рядов;

— вычеркивание нулевого ряда;

— прибавление к элементам некоторого ряда соответствующих элементов параллельного ряда, умноженных на любое действительное число.

Пример.

Теорема (необходимое и достаточное условие существования обратной матрицы).

Вычислить ранг матрицы

А =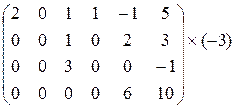

Решение. Преобразуем матрицу к ступенчатому виду. Для этого к третьей строке прибавим вторую, умноженную на (-3).

А ~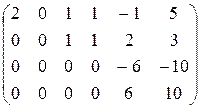

К четвертой строке прибавим третью.

А ~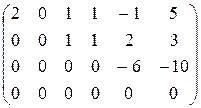

Число ненулевых строк в полученной эквивалентной матрице равно трем, следовательно r(А) = 3.

 

 

Системы n линейных уравнений с n неизвестными.

Методы их решения

Рассмотрим систему n линейных уравнений с n неизвестными.

а₁₁х₁ + а₁₂х₂ + … + а_1nx_n = b₁

а₂₁х₁ + а₂₂х₂ + … + а_2nx_n = b₂ (1)

……………………………….

а_n1х₁ + а_n2х₂ + … + а_nnx_n = b_n

 

Определение: Решением системы (1) называется совокупность чисел (х₁, х₂, …, х_n), которая обращает каждое уравнение системы в верное равенство.

Матрица А, составленная из коэффициентов при неизвестных, называется основной матрицей системы (1).

A =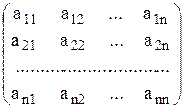

Матрица В, состоящая из элементов матрицы А и столбца свободных членов системы (1), называется расширенной матрицей.

В =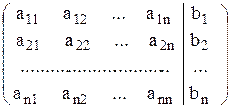

 

Матричный метод

Рассмотрим матрицы

Х = 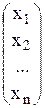— матрица неизвестных;

С = 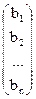— матрица свободных членов системы (1).

Тогда по правилу умножения матриц систему (1) можно представить в виде матричного уравнения

А × Х = С (2)

Решение уравнения (2) изложено выше, то есть Х = А^-1 × С, где А^-1 – обратная матрица для основной матрицы системы (1).

 

Метод Крамера

 

Система n линейных уравнений с n неизвестными, главный определитель которой отличен от нуля, всегда имеет решение и притом единственное, которое находится по формулам:

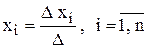
где D = det А – определитель основной матрицы А системы (1), который называется главным, Dх_i получаются из определителя D заменой i-ого столбца столбцом из свободных членов, т.е.

D = ;

Dх₁ = ;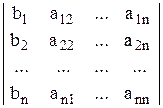

Dх₂ = ; … ;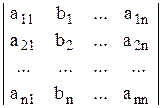

Dх_n = ;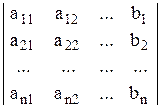

Пример.

Решить систему уравнений методом Крамера

 

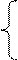2х₁ + 3х₂ + 4х₃ = 15

х₁ + х₂ + 5х₃ = 16

3х₁ — 2х₂ + х₃ = 1

Решение.

Вычислим определитель основной матрицы системы

D = det A = 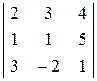= 44 ¹ 0

Вычислим вспомогательные определители

Dх₁ = 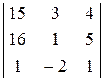= 0;

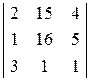Dх₂ = = 44;

Dх₃ = 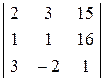= 132.

По формулам Крамера найдем неизвестные

; ; .

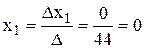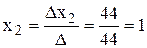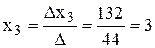Таким образом, х₁ = 0; х₂ = 1; х₃ = 3.

 

Метод Гаусса

 

Суть метода Гаусса заключается в последовательном исключении неизвестных из уравнений системы, т.е. в приведении основной матрицы системы к треугольному виду, когда под ее главной диагональю стоят нули. Это достигается с помощью элементарных преобразований матрицы над строчками. В результате таких преобразований не нарушается равносильность системы и она приобретает также треугольный вид, т.е. последнее уравнение содержит одну неизвестную, предпоследнее две и т.д. Выражая из последнего уравнения n-ую неизвестную и с помощью обратного хода, используя ряд последовательных подстановок, получают значения всех неизвестных.

Пример. Решить систему уравнений методом Гаусса

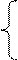3х₁ + 2х₂ + х₃ = 17

2х₁ — х₂ + 2х₃ = 8

х₁ + 4х₂ — 3х₃ = 9

Решение. Выпишем расширенную матрицу системы и приведем, содержащуюся в ней матрицу А к треугольному виду.

В =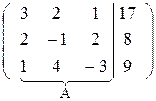

Поменяем местами первую и третью строки матрицы, что равносильно перестановке первого и третьего уравнений системы. Это позволит нам избежать появления дробных выражений при последующих вычислениях

В ~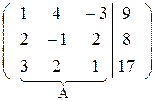

Первую строку полученной матрицы умножим последовательно на (-2) и (-3) и сложим соответственно со второй и третьей строками, при этом В будет иметь вид:

В ~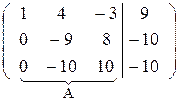

После умножения второй строки на 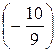и сложения ее с третьей строкой матрица А примет треугольный вид. Однако чтобы упростить вычисления можно поступить следующим образом: умножим третью строку на (-1) и сложим со второй. Тогда получим:

В ~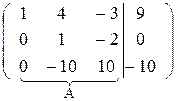

Далее, умножая вторую строку матрицы на 10 и складывая с третьей, окончательно получим:

В ~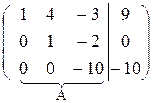

Восстановим из полученной матрицы В систему уравнений, равносильную данной

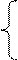х₁ + 4х₂ — 3х₃ = 9

х₂ — 2х₃ = 0

— 10х₃ = -10

Из последнего уравнения находим 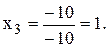Найденное значение х₃ = 1 подставим во второе уравнение системы, из которого х₂ = 2х₃ = 2 × 1 = 2.

После подстановки х₃ = 1 и х₂ = 2 в первое уравнение для х₁ получим х₁ = 9 — 4х₂ + 3х₃ = 9 — 4 × 2 + 3 × 1 = 4.

Итак, х₁ = 4, х₂ = 2, х₃ = 1.

Замечание. Для проверки правильности решения системы уравнений необходимо подставить найденные значения неизвестных в каждое из уравнений данной системы. При этом, если все уравнения обратятся в тождества, то система решена верно.

Проверка:

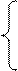3 × 4 + 2 × 2 + 1 = 17 верно

2 × 4 — 2 + 2 × 1 = 8 верно

4 + 4 × 2 — 3 × 1 = 9 верно

Итак, система решена верно.

 

⇐ Предыдущая1234Следующая ⇒

Читайте также:

Простейшие матричные уравнения

где – матрицы таких размеров, что все используемые операции возможны, а левые и правые части этих матричных уравнений представляют собой матрицы одинаковых размеров.

Решение уравнений (1)-(3) возможно с помощью обратных матриц в случае невырожденности матриц при Х. В общем случае матрицу Х записывают поэлементно и проводят указанные в уравнении действия над матрицами. В результате получают систему линейных уравнений. Решив систему, находят элементы матрицы Х.

Метод обратной матрицы

Это решение системы линейных уравнений в случае квадратной невырожденной матрицы системы А. Находится из матричного уравнения АХ=В.

А^-1(АХ)=А^-1В, (А^-1А)Х=А^-1В, ЕХ= А^-1В, Х= А^-1В.

 

Формулы Крамера

Теорема.Пусть Δ — определитель матрицы системы А, а Δ_j — определитель матрицы, получаемый из матрицы А заменой j-го столбцом свободных членов. Тогда, если Δ≠0, то система имеет единственное решение, определяемое по формулам:

— формулы Крамера.

ДЗ 1. 2.23, 2.27, 2.51,2.55, 2.62; ДЗ 2.2.19, 2.26, 2.40,2.65

Тема 4. Комплексные числа и многочлены

 

Комплексные числа и действия над ними

Определения.

1. Символ вида a + bi , где a и b произвольные действительные числа, условимся называть комплексным числом.

2. Комплексные числа a + bi и a₁ + b₁i условимся считать равными, если а = а₁ и

b = b₁.

3. Комплексное число вида a + 0i условимся считать равным действительному числу а.

4. Суммой двух комплексных чисел a + bi и a₁ + b₁i называется комплексное число (а + а₁) + (b + b₁)i.

5.

Обратная матрица. Ранг матрицы.

Произведением двух комплексных чисел называется комплексное число aa₁ – bb₁ + (a b₁ +a₁b)i.

Комплексное число вида 0 + bi называется чисто мнимым числом и обычно записывается так: bi; число 0 +1i = i называется мнимой единицей.

В силу определения 3 всякому действительному числу а соответствует «равное» комплексное число a + 0i и обратно – всякому комплексному числу a + 0i соответствует «равное» действительное число а, то есть между этими числами существует взаимно-однозначное соответствие. Если рассмотреть сумму и произведение комплексных чисел a₁ + 0i и a₂ + 0i по правилам 4 и 5, то получим:

(a₁ + 0i) + (a₂ + 0i) = (a₁ + a₂) + 0i,

(a₁ + 0i) (a₂ + 0i) = (a₁ a₂ – 0) + (a₁0+a₂0) i = a₁a₂ + 0i.

Мы видим, что сумме (или произведению) данных комплексных чисел соответствует действительное число, «равное» сумме (или произведению) соответствующих действительных чисел. Итак, соответствие между комплексными числами вида a + 0i и действительным числом а таково, что в результате выполнения арифметических действий над соответствующими компонентами получаются соответственные результаты. Взаимно-однозначное соответствие, которое сохраняется при выполнении действий, называется изоморфизмом. Это позволяет отождествить число a + 0i с действительным числом а и рассматривать всякое действительное число как частный случай комплексного.

Следствие. Квадрат числа i равен – 1.

i ² = i i = (0 +1i)( 0 +1i) = (0 – 1) + (0·1 + 1·0)i = — 1.

Теорема. Для сложения и умножения комплексных чисел остаются в силе основные законы действий.

Определения:

1. Действительное число а называется действительной частью комплексного числа z = a + bi. Rez=a

2. Число b называется мнимой частью комплексного числа z, число b — коэффициентом при мнимой части z. Imz=b.

3. Числа a + bi и a – bi называются сопряжёнными.

Число, сопряжённое числу z = a + bi обозначается символом

= a — bi.

Пример. z =3 + i , = 3 — i.

Теорема. Сумма и произведение двух сопряжённых комплексных чисел действительны.

Доказательство. Имеем

.

В множестве комплексных чисел выполнимы действия, обратные сложению и умножению.

Вычитание. Пусть z₁ = a₁ + b₁i и z₂ = a₂ + b₂i — данные комплексные числа. разность z₁ – z₂ есть число z = x + y i, удовлетворяющее условию z₁ = z₂ + z или

а₁ + b₁i = (a₂ + x) + (b₂ + y)i.

Для определения x и y получаем систему уравнений a₂ + x = а₁и b₂ + y = b₁, имеющую единственное решение:

x = а₁ — a₂, y = b₁ — b₂,

откуда

z = (а₁ + b₁i) – (а₂ + b₂i) = а₁ – а₂ +( b₁ — b₂)i.

Вычитание можно заменить сложением с числом, противоположным вычитаемому:

z = (а₁ + b₁i) – (а₂ + b₂i) = (а₁ + b₁i) + (- а₂ — b₂i).

Деление.

Частное чисел z₁ и z₂≠ 0 есть число z = x + y i , удовлетворяющее условию z₁ = z₂z или

а₁ + b₁i = (a₂ + b₂i) (x + yi),

следовательно,

а₁ + b₁i = a₂ x — b₂y+ (b₂x + a₂y)i,

откуда получаем систему уравнений:

a₂ x — b₂y = a₁,

b₂x + a₂y = b₁.

Решением которой будут

,

следовательно,

Практически для нахождения частного умножают делимое и делитель на число , сопряжённое делителю:

Так, например,

В частности число , обратное данному числу z , можно представить в виде

.

Примечание. В множестве комплексных чисел остаётся в силе теорема: еслипроизведение равно нулю, то хотя бы один из сомножителей равен нулю.

В самом деле, если z₁z₂ =0 и если z₁≠ 0, то умножая на , получим

что и требовалось доказать.

При выполнении арифметических действий над комплексными числами надлежит руководствоваться следующим общим правилом: действия выполняются по обычным правилам действий над алгебраическими выражениями с последующей заменой i² на -1.

Теорема. При замене каждого из компонентов сопряжённым ему числом результат действия тоже заменяется сопряжённым числом.

Доказательство заключается в непосредственной проверке. Так, например, если каждое слагаемое z₁ = a₁ + b₁i и z₂ = a₂ + b₂i заменить сопряжённым числом, то получим число, сопряжённое сумме z₁ + z₂.

cледовательно,

.

Аналогично для произведения имеем:

.

Предыдущая567891011121314151617181920Следующая

ПОСМОТРЕТЬ ЕЩЕ:

Матричные уравнения

Каталин Дэвид

AX = B, где матрица A обратима

Поскольку умножение матриц не всегда коммутативно, умножаем слева обе части уравнения на$ A^{-1}$.

$A^{-1}\cdot|A\cdot X = B$

$A^{-1}\cdot A\cdot X = A^{-1}\cdot B$

$I_{n}\cdot X = A^{-1}\cdot B$

Решение уравнения имеет общий вид
$\color{red}{X =A^{-1}\cdot B}$

Пример 50
Решить уравнение
$\begin{pmatrix} 1 & 3\\ 2 & 5 \end{pmatrix}\cdot X \begin{pmatrix} 3 & 5\\ 2 & 1 \end{pmatrix}$

Убедимся, что первая матрица обратима.
$\left|A\right|=5-6=-1\neq 0$, следовательно, матрица обратима.

Теорема 2. Критерий существования обратной матрицы.

Умножаем слева на обратную ей матрицу.
$\begin{pmatrix} 1 & 3\\ 2 & 5\\ \end{pmatrix}^{-1}\cdot \begin{pmatrix} 1 & 3\\ 2 & 5 \end{pmatrix}\cdot X= \begin{pmatrix} 1 & 3\\ 2 & 5 \end{pmatrix}^{-1}\cdot \begin{pmatrix} 3 & 5\\ 2 & 1 \end{pmatrix}$

$I_{2}\cdot X = \begin{pmatrix} 1 & 3\\ 2 & 5 \end{pmatrix}^{-1}\cdot \begin{pmatrix} 3 & 5\\ 2 & 1 \end{pmatrix}$

$X=\begin{pmatrix} 1 & 3\\ 2 & 5 \end{pmatrix}^{-1}\cdot \begin{pmatrix} 3 & 5\\ 2 & 1 \end{pmatrix}$

$\begin{pmatrix} 1 & 3\\ 2 & 5 \end{pmatrix}^{-1}= \begin{pmatrix} -5 & 3\\ 2 & -1 \end{pmatrix}\rightarrow X= \begin{pmatrix} -5 & 3\\ 2 & -1 \end{pmatrix}\cdot \begin{pmatrix} 3 & 5\\ 2 & 1 \end{pmatrix}= \begin{pmatrix} -9 & -22\\ 4 & 9 \end{pmatrix}$

XA = B, где матрица A обратима

Поскольку умножение матриц не всегда коммутативно, умножаем справа обе части уравнения на$ A^{-1}$.

$X\cdot A = B |\cdot A^{-1}$

$X\cdot A\cdot A^{-1} = B\cdot A^{-1}$

$X \cdot I_{n} =B\cdot A^{-1}$

Решение уравнения имеет общий вид
$\color{red}{X =B\cdot A^{-1}}$

Пример 51
Решить уравнение
$X \begin{pmatrix} 1 & 3\\ 2 & 5\\ \end{pmatrix}= \begin{pmatrix} 3 & 5\\ 2 & 1\\ \end{pmatrix}$

Убедимся, что первая матрица обратима.
$\left|A\right|=5-6=-1\neq 0$, следовательно, матрица обратима.

Умножаем справа на обратную ей матрицу.
$X \begin{pmatrix} 1 & 3\\ 2 & 5 \end{pmatrix}\cdot \begin{pmatrix} 1 & 3\\ 2 & 5 \end{pmatrix}^{-1}= \begin{pmatrix} 3 & 5\\ 2 & 1 \end{pmatrix}\cdot \begin{pmatrix} 1 & 3\\ 2 & 5 \end{pmatrix}^{-1}$

$X\cdot I_{2}= \begin{pmatrix} 3 & 5\\ 2 & 1 \end{pmatrix}\cdot \begin{pmatrix} 1 & 3\\ 2 & 5 \end{pmatrix}^{-1}$

$X=\begin{pmatrix} 3 & 5\\ 2 & 1 \end{pmatrix}\cdot \begin{pmatrix} 1 & 3\\ 2 & 5 \end{pmatrix}^{-1}$

$\begin{pmatrix} 1 & 3\\ 2 & 5 \end{pmatrix}^{-1}= \begin{pmatrix} -5 & 3\\ 2 & -1 \end{pmatrix}\rightarrow X= \begin{pmatrix} 3 & 5\\ 2 & 1 \end{pmatrix} \cdot \begin{pmatrix} -5 & 3\\ 2 & -1 \end{pmatrix}= \begin{pmatrix} -5 & 4\\ -8 & 5 \end{pmatrix}$

МатрицыУмножение матрицОпределителиРанг матрицыОбратные матрицыСистемы уравненийКалькуляторы для матриц

межд. изумления, удивления; радости, надежды; внезапности, испуга; горя, отчаяния. Ах, как хорошо! Ах кабы так! Ах, как ты меня испугал! Ах, да руками мах. Ах, ах, а пособить нечем. Ах, судья, судья: четыре полы, восемь карманов.

| Иногда ах обращается в сущ. , муж. Ахи, да охи, да бабьи вздохи. Что тут было ахов, удивления, радости. Ахти, ахти мне, восклицание горя, печали; увы; Ахти мне, все товарищи в тюрьме — что-то будет и мне? Охти-axmul как-то замуж идти? Не ахти мне, не на диво, не больно хорошо. Аханьки мне, ахаханьки, выражает как бы сострадание к самому себе, либо к другому. Аханьки, как детки махоньки, это род привета. Ахать, ахивать, ахнуть, дивиться; радоваться чему, горевать, стонать, восклицать ах! Ахал бы, да дома, по себе. Ахал бы дядя, на себя глядя, заботься всяк о себе, о своем деле. Я так и ахнул, испугался, изумился. Ахивали и мы, видывали горе. Холостой подчас охнет, а женатый ахнет.

Обратная матрица

Доахаться до чего. Заахали мы, узнав об этом. Наахали, да и пошли. Наахался я на чудеса эти. Отахали, что ли? Поахайте еще. Одна ахает, другая подахивает. Почто разахался? Взахаешься поневоле. Не так ахаешь, переахай снова, насмешка над бесполезными взывами. Весь денечек проахала. Пришла баба поахать, а пришлось охнуть; пришла поглядеть на чужую радость или горе, а приключилась своя беда. Аханье ср. неумеренное изъявление радости, изумления, горя, отчаянья: ахальщик муж. ахальщица жен. ахала об. кто всему дивится, выхваляет чужое не в меру, завидует. На каждого баяльщика по семи ахальщиков. На каждого бахаря по семи ахаль. Аховой ниж. ахтительный пенз. восхитительный, неимоверно прекрасный, красивый, вызывающий восклицание изумления и одобрения. Аховой платочек. Ахва? жен. , арх.-он. дыра, прореха; пробоина, прорез в шкуре, порча ее от неосторожного выстрела, укола или удара чем. Аховня? жен. испорченная ахвою шкура, аховая или ахводная шкура. Ахвить, ахводить?, испортить шкуру выстрелом, уколом, порубом. Аховая суббота, при платежах, когда неисправные ахают по деньгам.

Лемма: Для любой матрицы А произведение ее на единичную матрицу, соответствующего размера, равно матрице А: АЕ=ЕА=А.

Матрица В называется обратной к матрице А, если АВ=ВА=Е. Обратная матрица к матрице А обозначается А^-1.

Обратная матрица существует только для квадратной матрицы.

Теорема: Квадратная матрица А имеет обратную тогда и только тогда, когда определитель этой матрицы отличен от нуля (|A|≠0 ).

Алгоритм нахождения обратной матрицы А^-1:

(для матриц второго и третьего порядков)

1. Вычислить определитель данной матрицы (|A| ).
2. Если |A|≠0, то переходим к пункту 3.
   Если |A|=0, то обратная матрица не существует.
3. Вычислить все алгебраические дополнения A_ij элементов матрицы.
   

   Лекция 3. Свойства определителей. Обратная матрица

   ( Как это сделать можно посмотреть здесь)

4. Записать А^-1 по формуле:

   для матрицы второго порядка

   

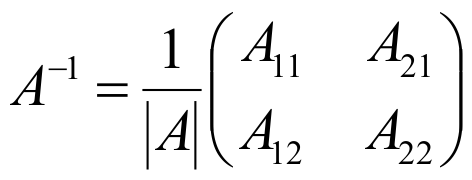
   и для матрицы третьего порядка

   

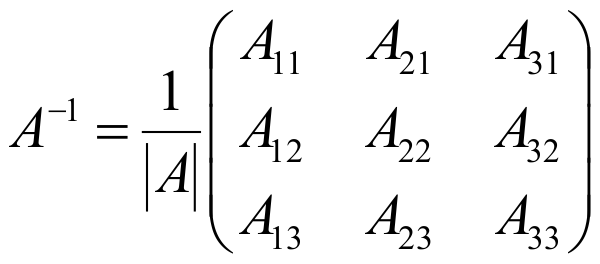
5. Сделать проверку: AA^-1 =A^-1A=E.

Для вычисления обратных матриц другого порядка изменится лишь формула в пункте 4.

Осталось заметить, что это не единственный способ нахождения обратной матрицы.

ПРИМЕРЫ:

Найти обратную матрицу для данных матриц:



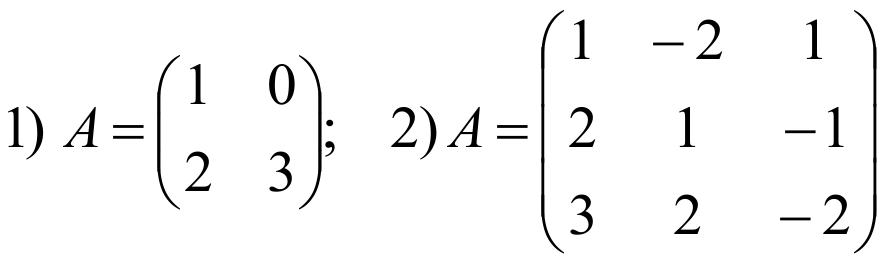
РЕШЕНИЕ:



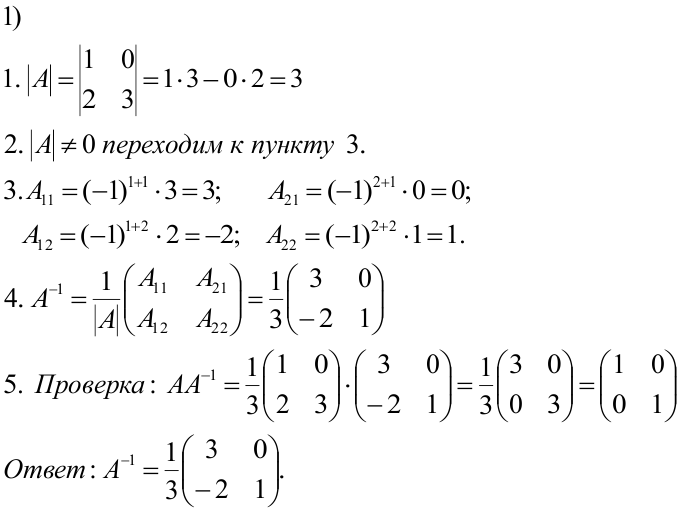
Упражнения к уроку:

Найти обратную матрицу для данных матриц:



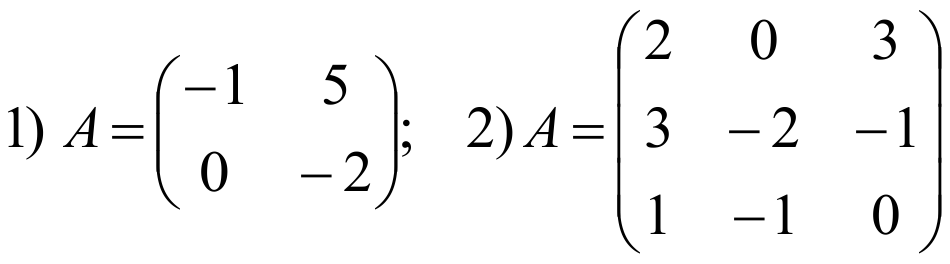
Показать ответ