Математика->Тригонометрия->тригонометрическая окружность->

Тестирование онлайн

Единичная окружность

Рассмотрим единичную окружность, т.е. окружность с центром в начале координат и радиусом, равным 1.

Каждой точке на единичной окружности соответствует угол, координата х и координата y.

Точке А соответствует угол ?=30⁰, координата х=0,87, координата y=0,5. Рассмотрим треугольник ОАВ: 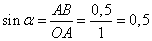; . Таким образом, координата х точки А — косинус угла ?, а координата y точки А — синус угла ?.

Для любой точки на окружности, соответствующей любому углу, можно определить значения косинуса и синуса этого угла.

Табличные значения углов

Знаки функций

Тригонометрическую окружность разбивают на четверти.

В соответствующей четверти синус, косинус, тангенс, котангенс принимают положительное или отрицательное значения.

Значение угла на тригонометрической окружности

При прохождении окружности против часовой стрелки, начиная с точки С (1;0), угол положительный, при прохождении по часовой стрелки — отрицательный.

В точку А можно попасть при повороте ОС на угол или на угол, отличающийся от на любое целое число оборотов. Например, или , или и т.д. Поэтому для описания угла, соответствующего точке А на окружности, применяют общую запись

В точку В можно попасть при повороте ОС на угол или, в общем виде, . Если угол, соответствующий точке В, описывать, используя положительное направление отсчета, получим эквивалентную запись .

Области значений тригонометрических функций

⇐ Предыдущая12345678Следующая ⇒

Как мы уже выяснили, чтобы найти синус числа на числовой окружности, нужно найти ординату точки, соответствующей этому числу (как это сделать?). А теперь обратим внимание, что проекции всех точек тригонометрической окружности укладываются на вертикальный диаметр, который является отрезком оси ординат. Т.к. концы этого отрезка по оси ординат имеют координатами числа (–1) и 1, то делаем вывод E(sin) = [–1; 1].

По-другому это записывается как или ,

говорят: «синус по модулю не превосходит единицу»,а вертикальный диаметр называется линией (осью) синусов.

 

Аналогично, рассматривая проекции абсцисс всех точек числовой окружности, делаем вывод, что E(cos) = [–1; 1].

Также как и для синуса, это можно записать в виде или ,

а линия (ось) косинусов — это горизонтальный диаметр.

Линия (ось) тангенсов — это касательная к числовой окружности, проходящая через ее начало отсчета.

Чтобы найти тангенс числа на числовой окружности нужно провести прямую через точку, соответствующую этому числу, и центр окружности до пересечения с линией тангенсов.

Масштаб по линии тангенсов такой же как и на числовой окружности (единичный отрезок – радиус окружности), поэтому тангенс числа равен длине отрезка от точки пересечения до точки касания.

Линия (ось) котангенсов — касательная, проведенная к числовой прямой через ее точку с координатой .

Для начала решим интересную задачу.

Задача.Какое из двух чисел больше, sin 1 или sin 2?

Вычисляют котангенс аналогично тангенсу, проводя прямую через центр числовой окружности и точку на ней и измеряя отрезок от точки пересечения до точки касания.

Таким образом, поскольку линия котангенсов – прямая, то E(ctg) = R.

С помощью линий тригонометрических функци, многие свойства тригонометрических функций получают наглядное геометрическое истолкование

Периодичность тригонометрических функций.Когда мы говорили об углах поворота, мы отметили их главную особенность – поворотам на углы, отличающиеся друг от друга на целое число полных оборотов (т.е. на 360°×п), соответствует одно и то же конечное положение подвижного радиус-вектора .

Это свойство синуса и косинуса называется периодичностью. Оно состоит в том, что от прибавления к аргументу х числа 2pk, где k – любое целое число, значения синуса и косинуса не изменяются.

Каждое из чисел ±2p, ±4p, ±6p, …, прибавление которого к любому значению аргумента х не изменяет значений синуса и косинуса, называют периодом синуса и косинуса. Из всех положительных периодов 2p, 4p, 6p,…, период 2p наименьший. Его называют главным периодом или просто периодом.

Свойство периодичности тангенса и котангенса в общем виде записывается как:

tg x = tg(x + pk) и ctg x = ctg(x + pk).Таким образом, периодами этих функций служат числа pk, а наименьший положительный период тангенса и котангенса равен p. Это следует из того, что на тригонометрической окружности точки tи t + p диаметрально противоположны (число p задает ровно половину окружности), а значит тангенсы этих чисел равны длине отрезка AN. Докажем, что наименьший период синуса 2p.Наибольшее значение синуса равно 1.

На числовой окружности этому значению соответствует точка В. Положение ОВ подвижный радиус сможет занять только через полный оборот, т.е. через 2p.

Вопрос 1.

Тригонометрический круг (окружность)

Как звучит это свойство применительно к точке на числовой окружности?

Вопрос 2. Чем являются координаты точки на числовой окружности?

Вопрос 3. Как записать правило «полного оборота» для каждой координаты?

sin x = sin(x + 2pk) и cos x = cos(x + 2pk).

Четность и нечетность.

Еще проще с таким важным свойством функций как четность или нечетность.

Оказывается, все изучаемые нами тригонометрические функции – нечетные, лишь косинус – четная функция.

Рассмотрим на тригонометрической окружности точки с координатами t и (–t). У этих точек равные по модулю, но противоположные по знаку ординаты, это означает, что sin(–t) = –sin t. У таких точек одна и та же абсцисса, а это значит, что cos(–t) = cos t.

Аналогично рассматриваются функции тангенс и котангенс.

Кроме того, доказать нечетность тангенса и котангенса можно используя свойства синуса и косинуса следующим образом: = = = — = — .

---

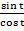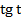⇐ Предыдущая12345678Следующая ⇒

---

Дата добавления: 2016-03-26; просмотров: 710 | Нарушение авторских прав

---

Похожая информация:

Поиск на сайте:

Тригонометрический круг. Единичная окружность. Числовая окружность. Что это такое?

Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень…»
И для тех, кто «очень даже…» )

 

Очень часто термины тригонометрический круг, единичная окружность, числовая окружность плохо понимаются учащимся народом. И совершенно зря. Эти понятия – мощный и универсальный помощник во всех разделах тригонометрии. Фактически, это легальная шпаргалка! Нарисовал тригонометрический круг – и сразу увидел ответы! Заманчиво? Так давайте освоим, грех такой вещью не воспользоваться. Тем более, это совсем несложно.

Для успешной работы с тригонометрическим кругом нужно знать всего три вещи.

Первое. Надо знать, что такое синус, косинус, тангенс и котангенс в применении к прямоугольному треугольнику. Сходите по ссылке, кто ещё не был. Тогда и здесь всё ясно будет.

Второе. Надо знать, что такое тригонометрический круг, единичная окружность, числовая окружность. Это я расскажу прямо здесь и сейчас.

Третье. Надо знать, как отсчитывать углы на тригонометрическом круге, и что такое градусная и радианная меры углов. Это будет в следующих уроках.

Всё. Разобравшись с этими тремя китами, получим надёжную, безотказную и совершенно законную шпаргалку для всей тригонометрии сразу.

А то в школьных учебниках с этой самым тригонометрическим кругом как-то не очень…

Начнём, помаленьку.

В предыдущем уроке вы усвоили, что синус, косинус, тангенс и котангенс (т.е.

тригонометрические функции) зависят только от угла. И не зависят от длин сторон в прямоугольном треугольнике. Отсюда интересный вопрос. Пусть у нас есть вот такой угол. Назовём его угол β. Буква красивая.)

Раз есть угол, у него должны быть тригонометрические функции! Синус, скажем, или котангенс… А где их взять? Нет ни гипотенузы, ни катетов…

Как определить тригонометрические функции угла без прямоугольного треугольника? Задачка… Придётся опять лезть в сокровищницу мировых знаний. К средневековым людям. Те всё умели…

Первым делом возьмём координатную плоскость. Это самые обычные координатные оси, ОХ – по горизонтали, ОY – по вертикали. И… прибьём одну сторону угла к положительной полуоси ОХ. Вершина угла, естественно, в точке О. Крепко прибьём, чтобы не оторвать! Вторую сторону оставим подвижной, чтобы угол менять можно было. Раздвижной у нас угол будет. Конец неприбитой стороны угла обозначим точкой А. Получим вот такую картинку:

 

 

Так, угол пристроили. А где его синус, где косинус? Спокойно! Сейчас всё будет.

Отметим координаты точки А на осях. Наведите курсор мышки на картинку и всё увидите. На ОХ это будет точка В, на ОY — точка С. Понятно, что В и С — это какие-то числа. Координаты точки А.

Так вот, число В будет косинусом угла β, а число С – его синусом!

С чего бы это? Древние люди учили нас, что синус и косинус – это отношения сторон! Которые от длин сторон не зависят. А мы тут координаты точки придумали… Но! Посмотрите на треугольник ОАВ. Прямоугольный, кстати… По древнему определению косинус угла β равен отношению прилежащего катета к гипотенузе. Т.е. ОВ/ОА. Ладно, не возражаем. Причём косинус и синус не зависят от длин сторон.

Синус, косинус, тангенс и котангенс. Тригонометрический круг

А это вообще отлично! Это значит, что длины сторон можно брать какие угодно. Имеем полное право взять длину ОА за единицу! Неважно чего. Хоть метр, хоть километр, всё равно синус не меняется. А в этом случае

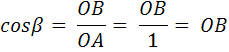
Вот так. Если провести такие же рассуждения для синуса, получим, что синус угла β равен АВ. Но АБ = ОС. Следовательно,

Можно сказать совсем просто. Синусом угла β будет игрековая координата точки А, а косинусом – иксовая. Слова нестандартные, но тем лучше. Запоминается надёжнее! А запомнить это надо. Железно запомнить. Косинус – по иксу, синус – по игреку.

Нет, не обидели средневековые люди древних! Сберегли наследие! И отношение сторон сохранили, и возможности расширили чрезвычайно!

Однако, а где тригонометрический круг!? Где единичная окружность!? Ни слова про круги не было!

Верно. Но осталось всего ничего. Взять подвижную сторону ОА и повернуть её вокруг точки О на полный оборот. Как вы думаете, какую фигуру нарисует при этом точка А? Совершенно верно! Окружность! Вот она.

Вот это и будет тригонометрический круг.

Вот так. А почему круг — тригонометрический? Круг и круг… Вопрос резонный. Поясняю. Каждой точке окружности соответствуют два числа. Координата этой точки по Х и координата этой точки по Y. А координаты у нас что? Наведите курсор на рисунок. Координаты у нас — точки В и С. Т.е. косинус и синус угла β. Т.е. тригонометрические функции. Поэтому круг и называется тригонометрическим.

Вспомнив, что ОА = 1, а ОА – радиус, сообразим, что это же – и единичная окружность тоже.

А так как синус и косинус — просто какие-то числа — этот тригонометрический круг будет ещё и числовой окружностью.

Три термина в одном флаконе.)

В данной теме эти понятия: тригонометрический круг, единичная окружность и числовая окружность – одно и то же. В более широком смысле, единичная окружность – это любая окружность с радиусом, равным единице. Тригонометрический круг – практический термин, как раз для работы с единичной окружностью в тригонометрии. Чем мы сейчас и позанимаемся. Работой с тригонометрическим кругом.

Первую половину работы мы уже выполнили. Нарисовали тригонометрический круг с помощью угла (классно звучит, правда?).

Теперь выполним вторую половину работы. Сделаем то же самое, только наоборот. Пройдём путь от тригонометрического круга к углу.

Пусть нам дана единичная окружность. Т.е. просто окружность, нарисованная на координатной плоскости, с радиусом, равным единице. Возьмём произвольно точку А на окружности. Отметим её координаты точками В и С на осях. Как нам помнится, её координаты — это cosβ (по иксу) и sinβ (по игреку). И синус с косинусом отметим. Получим вот такую картинку:

Всё понятно? Внимание, вопрос!

Где β!? Где угол β, без которого синуса и косинуса не бывает!?

Наводим курсор на картинку, и… вот он, вот он угол β! Именно его синус и косинус являются координатами точки А.

Кстати, здесь не нарисована прибитая сторона угла. Она и в предыдущих рисунках не нужна, только так, для понимания… Угол всегда отсчитывается от положительного направления оси ОХ. От направления стрелки.

А если точку А взять в другом месте? Окружность — она круглая… Да пожалуйста! Где угодно! Поместим, к примеру, точку А во вторую четверть, отметим её координаты, синус, косинус, как полагается. Вот так:

Самые наблюдательные заметят, что синус угла β – положительный (точка С – на положительной полуоси OY), а вот косинус – отрицательный! Точка В лежит на отрицательной полуоси ОХ.

Наводим курсор на картинку и видим угол β. Угол β здесь – тупой. Чего, кстати, решительно не бывет в прямоугольном треугольнике. А зря, что ли, мы возможности расширяли?

Уловили суть тригонометрического круга? Если взять точку в любом месте окружности, её координатами будут косинус и синус угла. Угол отсчитывается от положительного направления оси ОХ и до прямой, соединяющей центр координат с этой самой точкой на окружности.

Вот и всё. Проще хотелось бы, да некуда. Кстати, мой вам совет. Работая с тригонометрическим кругом, рисуйте не только точки на окружности, но и сам угол! Как на этих рисунках. Понятнее будет.

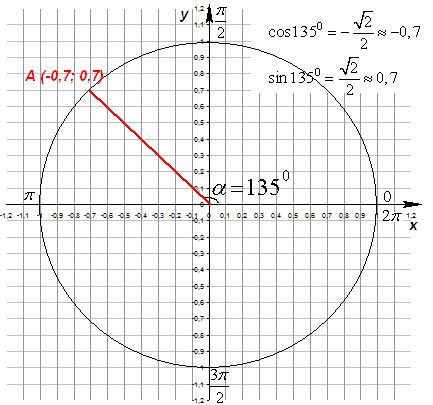
Рисовать вам этот круг в тригонометрии постоянно придётся. Это не обязаловка, это и есть та легальная шпаргалка, которой пользуются умные люди. Сомневаетсь? Тогда назовите мне по памяти знаки вот таких выражений, к примеру: sin130⁰, cos150⁰, sin250⁰, cos330⁰? Я уж не спрашиваю про cos1050⁰ или sin(-145⁰)… Про такие углы в следующем уроке написано.

И нигде-то вы подсказку не найдёте. Только на тригонометрическом круге. Рисуем примерный угол в правильной четверти и сразу видим, куда попадают его синус и косинус. На положительные полуоси, или отрицательные. Кстати, определение знаков тригонометрических функций постоянно требуется в самых различных заданиях…

Или ещё, чисто для примера… Надо вам, например, узнать, что больше, sin130⁰, или sin155⁰? Попробуй-ка, сообрази просто так…

А мы умные, мы нарисуем тригонометрический круг. И нарисуем на нём угол примерно 130 градусов. Исходя только из того, что он больше 90 и меньше 180 градусов. Ориентируемся на угол, а не на окружность! Уж где пересечёт подвижная сторона угла окружность, там и пересечёт. Отмечаем игрековую координату точки пересечения. Это будет sin130⁰. Как на этом рисунке:

А затем, здесь же, нарисуем угол 155 градусов. Примерно нарисуем, зная, что он больше 130 градусов. И меньше 180. Отметим и его синус. Наведите курсор на картинку, всё увидите. Ну и что, какой синус больше? Тут уж совсем трудно ошибиться! Конечно sin130⁰ больше, чем sin155⁰!

Долго? Да ну?! Никто не требует от вас тщательно прорисовывать картину и обеспечивать мультипликацию! Поработаете с этим сайтом, и по этой задаче будете за 10 секунд рисовать вот такую картинку:

Другой и не сообразит, что это за каракули, да… А вы спокойно и уверенно дадите правильный ответ! Хотя, аккуратность и не мешает… А то можно такую «окружность» нарисовать, что ответ обратный получится…

Эта задачка — только один пример широких возможностей тригонометрического круга. Освоить эти возможности вполне реально. Чем мы и займёмся далее.

Чаще всего вам придётся иметь с тригонометрическими функциями в обычной, алгебраической записи. Типа sin45⁰, tg(-3), cos(x+y) и так далее. Безо всяких картинок и тригонометрических кругов! Рисовать этот самый круг надо самим. Руками. Если, конечно, хотите легко и правильно решать задания по тригонометрии. В том числе и самые продвинутые. Но особо не волнуйтесь. Уж на этом сайте, в тригонометрии, я вам обеспечу рисование кругов! И вы освоите этот крайне полезный приём. Однозначно.

Подведём итоги урока.

В этой теме мы плавно перешли от тригонометрических функций угла в прямоугольном треугольнике к тригонометрическим функциям любого угла. Для этого нам понадобилось освоить понятия «тригонометрический круг, единичная окружность, числовая окружность». Это очень полезно.)

Здесь я рассказывал о тригонометрическом круге в применении к синусу и косинусу. Но тангенс и котангенс тоже можно увидеть на круге! Одно движение ручкой, и вы легко и правильно определяете знак тангенса — котангенса любого угла, решаете тригонометрические неравенства и вообще потрясаете окружающих своими тригонометрическими способностями.)

Если вас интересуют такие перспективы — можно посетить урок «Тангенс и котангенс на тригонометрическом круге» в Особом разделе 555.

Далее мы разберёмся со следующими вопросами.

Как выглядят углы в 1000 градусов? Как выглядят отрицательные углы? Что за загадочное число «Пи», на которое неизбежно наталкиваешься в любом разделе тригонометрии? И каким боком это «Пи» к углам пристраивается? Всё это – в следующих уроках.

---

Нестрашная математика для всех:
научиться не бояться, понимать и любить!

Для дошкольников и младших школьников: научиться быстро считать, решать головоломки, развить логику и умение рассуждать.

Для школьников «гуманитарного склада ума»: перестать бояться математики, понять базовые принципы, найти свой подход к решению задач, улучшить школьные оценки.

Для взрослых: по-новому посмотреть на математику, научиться решать задачи, говорить про математику с детьми, освоить инструментарий
для решения взрослых профессиональных задач.

Тригонометричне коло.Cуховерхова Л.П.

Author channel Людмила Суховерхова   6 год. назад

Одиничне КОЛО! Тригонометрія. Дуже доступно! Ч.1

Перша частина складної теми «Одиничне коло». Продивившись усі частини ви зрозумієте ЯК ВРЕШТІ РЕШТ РАХУВАНИ СИНУСИ КОСІНУСИ ПО ОДИНИЧНОМУ КОЛІ. Приємного перегляду 😉

🔴 Тригонометрия (начало)

Подпишись! Скачать табличку: https://docs.google.com/file/d/0B0rPijkOBg-INW81Tm1lZzNDbnM/edit Наш канал: http://youtube.com/user/ShkolaPifagora Наша группа вконтакте: http://vk.com/shkolapifagora Сайт: http://школапифагора.рф Список тем: 00:35 | Название координатных осей 01:01 | Почему окружность называют единичной? 01:35 | Начало тригонометрической окружности 01:49 | Где находится первая, вторая, третья и четвёртая четверти? 04:35 | Как ходить по тригонометрической окружности? 04:46 | Где находится 90 градусов? 05:14 | Где находится 180 градусов?

Тригонометрический круг и формулы

05:30 | Где находится 270 градусов? 05:48 | Где находится 360, 450, 540, 630, 720, 810 и т.д. градусов? 06:24 | Чему равно число Пи в числовом значении? 06:42 | Чему равно число Пи в градусах? 06:57 | В каком месте окружности находится число Пи (180 градусов)? 07:21 | В каком месте окружности находится число Пи/2 (90 градусов)? 07:41 | В каком месте окружности находится число 3Пи/2 (270 градусов)? 08:12 | В каком месте окружности находится число Пи/6 (30 градусов)? 10:05 | В каком месте окружности находится число Пи/4 (45 градусов)? 10:42 | В каком месте окружности находится число Пи/3 (60 градусов)? 11:26 | В каком месте окружности находится число 2Пи/3 (120 градусов)? 12:04 | В каком месте окружности находится число 3Пи/4 (135 градусов)? 13:02 | В каком месте окружности находится число 5Пи/6 (150 градусов)? 13:53 | В каком месте окружности находится число 7Пи/6 (210 градусов)? 14:37 | В каком месте окружности находится число 5Пи/4 (225 градусов)? 15:32 | В каком месте окружности находится число 4Пи/3 (240 градусов)? 16:22 | В каком месте окружности находится число 5Пи/3 (300 градусов)? 17:01 | В каком месте окружности находится число 7Пи/4 (315 градусов)? 17:47 | В каком месте окружности находится число 11Пи/6 (330 градусов)? 18:30 | Как найти любое тригонометрическое значение? 19:35 | 3 равенства, которые надо выучить 21:05 | Отмечаем эти 3 значения на оси косинуса (абсциссе) и оси игрека (ординате) 23:23 | Отмечаем отрицательные значения на оси косинуса (абсциссе) и оси игрека (ординате) 24:50 | Как найти sin 3Пи/2? 25:40 | Как найти cos 23Пи/6? 27:58 | Как найти sin 323Пи/6? 30:38 | Как найти cos 315 градусов? 31:25 | Как найти sin 660 градусов? 32:18 | Как найти cos 3630 градусов? 33:50 | Как найти sin или cos отрицательного аргумента? 34:24 | Как найти sin (-3Пи/2)? 35:11 | Как найти cos (-23Пи/6)? 36:53 | Как найти sin (-323Пи/6)? 38:06 | Как найти cos (-315) градусов? 38:54 | Как найти sin (-660) градусов? 39:53 | Как найти cos (-3630) градусов? 41:07 | Как найти tg или ctg? 42:08 | Как найти tg 45 градусов? 43:04 | Как найти ctg 510 градусов? 44:52 | Как найти tg (-300) градусов? 46:16 | Как найти ctg (-690) градусов? 47:43 | Определяем знаки синуса 48:10 | Определяем знаки косинуса 48:34 | Определяем знаки тангенса и котангенса

Одиничне коло (СІНУС & КОСИНУС) Part 3

Як же по одиничному колу знаходити сінус, косинус, тангенс котангенс) Дуже доступно пояснюю!!!!

Тригонометрическая окружность

Отдельные разделы тригонометрии рассеяны по всему школьному курсу математики. А мы собрали их все вместе и рассказываем за девять 10-минутных уроков: от исчисления углов в прямоугольном треугольнике до теоремы косинусов. Самый сложный раздел школьной тригонометрии — это вывод формул синуса и косинуса суммы двух углов. Когда вы разберётесь с этим разделом, вы без большого труда справитесь и со всем остальным.

Градусная мера угла. Тригонометрия (01 — 01)

Первая часть урока «Градусная и радианная мера угла» курса «Тригонометрия». Дополнительные материалы на сайте http://ongradient.com

Окружность

Окружность — геометрическое место точек плоскости, расстояние от которых до центра окружности равно.

Центр окръжности

Радиус: расстояние от центра окружности до его границы.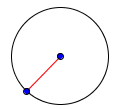

Диаметр: наибольшее расстояние от одной границы окружности до другой. Диаметр равен двум радиусам.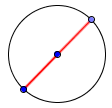

Периметр (длина окружности): длина границы окружности.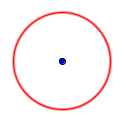

Длина окружности $= \pi \times$ диаметр

$\pi$ — pi: число, равное 3.141592… или $\approx \frac{22}{7}$, то есть отношение $\frac{\text{длины окружности}}{\text{диаметр}}$ любого окружности.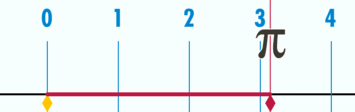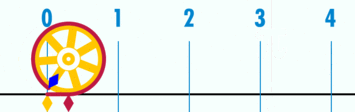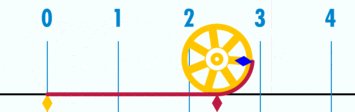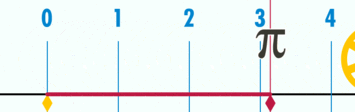

Дуга: изогнутая линия, которая является частью окружности.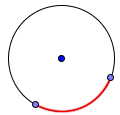

Дуги окружности измеряется в градусах или радианах. Например: 90° или $\frac{\pi}{2}$ — четверть круга, 180° или $\pi$ — половина круга.
Сумма всех дуг окружности составляет 360°

Хорда: отрезок прямой, соединяющей две точки на окружности.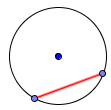

Сектор: похож на часть пирога (клин).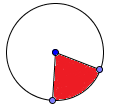

Касательная к окружности: прямая, перпендикулярна к радиусу, и имеющая ТОЛЬКО одну общую точку с окуржностью.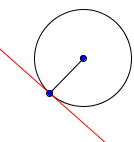

Формулы

Длина окружности $=\pi \cdot \text{диаметр} = 2\cdot \pi \cdot \text{радиус}$

Площадь круга $= \pi \cdot$ радиус²

Радиус обозначается как r, диаметр как d, длина окружности как P и площадь как S.

$P = \pi \cdot d = 2\cdot \pi \cdot r$
$S = \pi \cdot r^2$

Площадь сектора круга

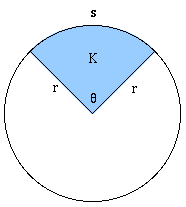
Площадь сектора круга K: (с центральным углом $\theta$ и радиусом $r$).
Если угол $\theta$ в градусах, тогда площадь = $\frac{\theta}{360} \pi r^2$
Если угол $\theta$ в радианах, тогда площадь, тогда площадь = $\frac{\theta}{2} r^2$

Углы

Центральный угол

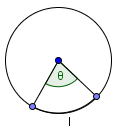
Если длина дуги составляет $\theta$ градуов или радиан, то значение центрального угла также $\theta$ (градусов или радиан).

Если вы знаете длину дуги (в дюймах, ярдах, футах, сантиметрах, метрах …) вы можете найти значение её соответствующего центрального угла ($\theta$) по формуле:

$\theta = 360 \cdot \frac{l}{P} = \frac{360 \cdot l}{2 \cdot \pi \cdot r} = \frac{180 \cdot l}{\pi \cdot r}$

$l$ — длина дуги.

Вписанный угол

Вписанный угол это угол с вершиной на окружности и со сторонами, которые содержат хорды окружности.

Тригонометрический круг: вся тригонометрия на одном рисунке

На рисунке, угол APB это вписанный угол.

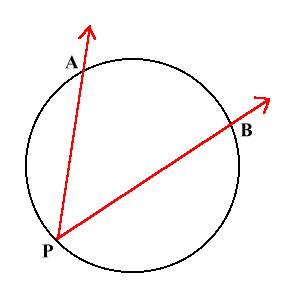
Величина вписанного угла равна половине дуги, на которую он опирается.

Пример:
$\widehat{AB} = 84^\circ$
$\angle APB = \frac{84}{2} = 42^\circ$

Углы между двумя хордами

Случай 1: два секущие пересекаются внутри окружности.

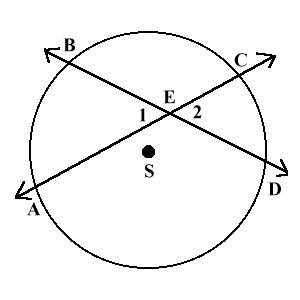
Когда две секущие пересекаются внутри окружности, величина образованных угла, в два раза меньше суммы величин дуг, на которые они опираются. На рисунке дуга AB и дуга CD равны 60° и 50° тогда углы 1 и 2 равны $\frac{1}{2}(60^\circ + 50^\circ)=55^\circ$

Случай 2: две секущие пересекаются вне окружности.

Иногда секущие пересекаются за пределами окружности. Когда это случается, величина образующихся углов равна половине разности дуг, на которые они опираются.

$\angle ABC =\frac{1}{2}(x — y)$

На рисунке дуга AB=80° и дуги CD=30°.
$\angle ABC = \frac{1}{2}(80 — 30) = \frac{1}{2} \cdot 50 = 25^\circ$

Хорды

Если две хорды пересекаются внутри окружности, как на рисунке выше, тогда:

$AX \cdot XB = CX \cdot XD$