tgx • ctgx = 1

tg2x + 1	=	1
cos2x

ctg2x + 1	=	1
sin2x

Формулы сложения и вычитания:

sin(x + y) = sinx cosy + cosx siny
cos(x + y) = cosx cosy — sinx siny

tg(x + y)	=	tgx + tgy
1 — tgx tgy

ctg(x + y)	=	ctgx ctgy — 1
ctgx + ctgy

sin(x — y) = sinx cosy — cosx siny
cos(x — y) = cosx cosy + sinx siny

tg(x — y)	=	tgx — tgy
1 + tgx tgy

ctg(x — y)	=	ctgx ctgy + 1
ctgx — ctgy

Формулы двойных углов:

sin2x = 2sinx • cosx

cos2x = cos² — sin²x = 2cos²x — 1 = 1 — 2sin²x

tg2x	=	2tgx	=	2ctgx	=	2
1 — tg2x	ctg2x — 1	ctgx — tgx

ctg2x	=	ctg2x — 1	=	ctgx — tgx
2ctgx	2

Формулы понижения степени:

sin2x	=	1 — cos2x
2

cos2x	=	1 + cos2x
2

Формулы половинного аргумента:

sin2	x	=	1 — cosx
2	2

cos2	x	=	1 + cosx
2	2

tg2	x	=	1 — cosx
2	1 + cosx

ctg2	x	=	1 + cosx
2	1 — cosx

tg	x	=	1 — cosx	=	sinx
2	sinx	1 + cosx

ctg	x	=	1 + cosx	=	sinx
2	sinx	1 — cosx

Преобразование суммы (разности) функций в произведение:

1. Сумма:

sinx + siny	=  2sin	x + y	• cos	x — y
2	2

cosx + cosy	=  2cos	x + y	• cos	x — y
2	2

(sinx + cosx)² = 1 + sin2x

tgx + tgy	=	sin(x + y)
cosx • cosy

ctgx + ctgy	=	sin(x + y)
sinx • siny

2. Разность:

sinx — siny	=  2sin	x — y	• cos	x + y
2	2

cosx — cosy	=  -2sin	x + y	• sin	x — y
2	2

(sinx — cosx)² = 1 — sin2x

tgx — tgy	=	sin(x — y)
cosx • cosy

ctgx — ctgy	=  –	sin(x — y)
sinx • siny

Преобразование произведения тригонометрических функций в сумму:

sinx • siny	=	cos(x — y) — cos(x + y)
2

sinx • cosy	=	sin(x — y) + sin(x + y)
2

cosx • cosy	=	cos(x — y) + cos(x + y)
2

Соотношения между обратными тригонометрическими функциями:

Способов для вычисления значения выражения cos п достаточно, поэтому рассмотрим некоторые из них.

1. По таблице значений косинуса

Один из самых простых способов — это использование таблицы, в которой собраны значения четырех основных тригонометрических функций от основных аргументов.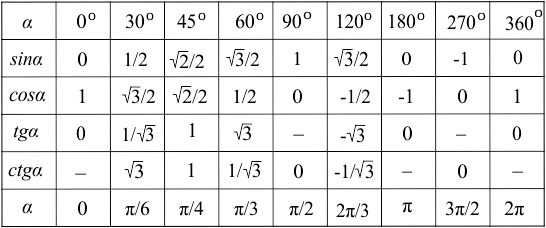

В таблице значения аргументов могут быть представлены в виде градусов или в виде радиан. Поскольку в задании аргументы даны в радианах, то по таблице найдем столбец, в котором находится значение Пи.

Решите уравнение cos x=-1/2

В первом столбце обратим внимание на функции — нас интересует косинус. На пересечении этих двух данных получим результат — значение косинуса Пи.
Итак, косинус Пи согласно таблице равен —1:

   

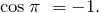
1. По тригонометрическому кругу

Можно вычислять значения тригонометрических функций по тригонометрическому кругу (или окружности).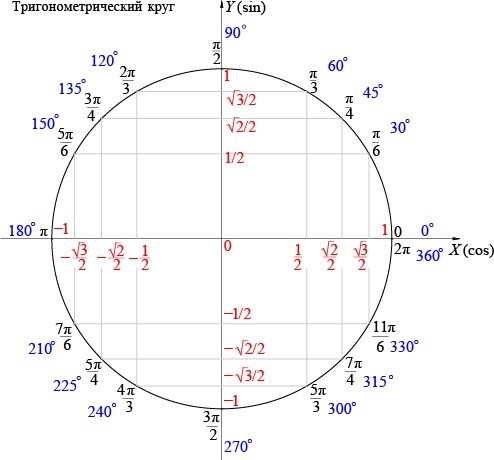

На осях круга содержаться значения двух тригонометрических функций: на оси Ох — значения косинусов, а на оси Оу — значения синусов.
Найдем на самой окружности значение, которое соответствует аргументу функции, то есть Пи. Число 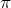на оси Ох лежит в точке —1. Таким образом, косинус равен —1.

1. По графику косинуса

Для основных углов удобно находить значения функций с помощью графика соответствующей функции.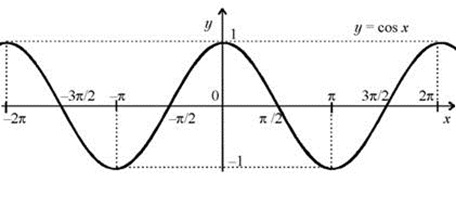

По косинусоиде (так называется график косинуса) отчетливо видно, что косинус равен —1.

Уравнение sin x = a.
Уравнение cosx = a.
Уравнение tgx = a.
Уравнение ctg x = a.
Формулы, таблицы значений, примеры, пояснения.

 

Уравнение sin x = a

 

Условия:

1) | a | ≤ 1

2) при | a | > 1 уравнение sin x = a не имеет решения среди действительных чисел.

 

Формула решения уравнения sin x = a:

x = (-1)n · arcsin α + πn   где n – любое целое число (n ∈ Z).

 

 

 

 

 

 

 

 

 

 

Ответ оставил Гость

3x — неизвестная и она будет равна значению угла в точке 0

а чтобы найти x, нужно обе части поделить на 3

представляем это как 1/3.

обе части делим на 1/3. 0 делить на 1/3 так и будет ноль.

cosx=-1

впринципе табличное значение. но вообще хорошо бы представлять себе тригонометрический круг. косинус на оси x. отмеряем -1 на оси x. чтобы спроецировать -1 на ось икс, на нужно пройти 180 градусов по часовой стрелке или π, в радианах. добавим сюда ещё период косинуса 2π*k

опять же делаем как первом примере

2x приравниваем к значению угла в √2/2

Но это все — таличные значения, их нужно просто выучить.

Знаки тригонометрических функций

Знак тригонометрической функции зависит исключительно от координатной четверти, в которой располагается числовой аргумент. В прошлый раз мы учились переводить аргументы из радианной меры в градусную (см. урок «Радианная и градусная мера угла»), а затем определять эту самую координатную четверть. Теперь займемся, собственно, определением знака синуса, косинуса и тангенса.

угла α — это ордината (координата y ) точки на тригонометрической окружности, которая возникает при повороте радиуса на угол α.

угла α — это абсцисса (координата x ) точки на тригонометрической окружности, которая возникает при повороте радиуса на угол α.

угла α — это отношение синуса к косинусу. Или, что то же самое, отношение координаты y к координате x .

Обозначение: sin α = y ; cos α = x ; tg α = y : x .

Все эти определения знакомы вам из курса алгебры старших классов. Однако нас интересуют не сами определения, а следствия, которые возникают на тригонометрической окружности. Взгляните:

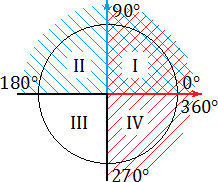
Синим цветом обозначено положительное направление оси OY (ось ординат), красным — положительное направление оси OX (ось абсцисс). На этом «радаре» знаки тригонометрических функций становятся очевидными. В частности:

1. sin α > 0, если угол α лежит в I или II координатной четверти. Это происходит из-за того, что по определению синус — это ордината (координата y ). А координата y будет положительной именно в I и II координатных четвертях;
2. cos α > 0, если угол α лежит в I или IV координатной четверти. Потому что только там координата x (она же — абсцисса) будет больше нуля;
3. tg α > 0, если угол α лежит в I или III координатной четверти. Это следует из определения: ведь tg α = y : x , поэтому он положителен лишь там, где знаки x и y совпадают. Это происходит в I координатной четверти (здесь x > 0, y > 0) и III координатной четверти ( x < 0, y < 0).

Для наглядности отметим знаки каждой тригонометрической функции — синуса, косинуса и тангенса — на отдельных «радарах». Получим следующую картинку:

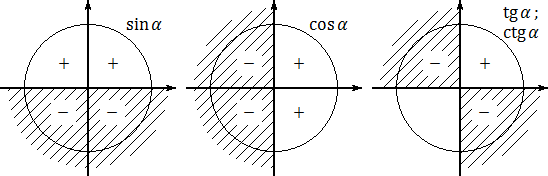
Заметьте: в своих рассуждениях я ни разу не говорил о четвертой тригонометрической функции — котангенсе. Дело в том, что знаки котангенса совпадают со знаками тангенса — никаких специальных правил там нет.

Теперь предлагаю рассмотреть примеры, похожие на задачи B11 из пробного ЕГЭ по математике, который проходил 27 сентября 2011. Ведь лучший способ понять теорию — это практика.

Желательно — много практики. Разумеется, условия задач были немного изменены.

Задача. Определите знаки тригонометрических функций и выражений (значения самих функций считать не надо):

1. sin (3π/4);
2. cos (7π/6);
3. tg (5π/3);
4. sin (3π/4) · cos (5π/6);
5. cos (2π/3) · tg (π/4);
6. sin (5π/6) · cos (7π/4);
7. tg (3π/4) · cos (5π/3);
8. ctg (4π/3) · tg (π/6).

План действий такой: сначала переводим все углы из радианной меры в градусную (π → 180°), а затем смотрим в какой координатной четверти лежит полученное число. Зная четверти, мы легко найдем знаки — по только что описанным правилам. Имеем:

1. sin (3π/4) = sin (3 · 180°/4) = sin 135°. Поскольку 135° ∈ [90°; 180°], это угол из II координатной четверти. Но синус во II четверти положителен, поэтому sin (3π/4) > 0;
2. cos (7π/6) = cos (7 · 180°/6) = cos 210°. Т.к. 210° ∈ [180°; 270°], это угол из III координатной четверти, в которой все косинусы отрицательны. Следовательно, cos (7π/6) < 0;
3. tg (5π/3) = tg (5 · 180°/3) = tg 300°. Поскольку 300° ∈ [270°; 360°], мы находимся в IV четверти, где тангенс принимает отрицательные значения. Поэтому tg (5π/3) < 0;
4. sin (3π/4) · cos (5π/6) = sin (3 · 180°/4) · cos (5 · 180°/6) = sin 135° · cos 150°. Разберемся с синусом: т.к. 135° ∈ [90°; 180°], это II четверть, в которой синусы положительны, т.е. sin (3π/4) > 0. Теперь работаем с косинусом: 150° ∈ [90°; 180°] — снова II четверть, косинусы там отрицательны. Поэтому cos (5π/6) < 0. Наконец, следуя правилу «плюс на минус дает знак минус», получаем: sin (3π/4) · cos (5π/6) < 0;
5. cos (2π/3) · tg (π/4) = cos (2 · 180°/3) · tg (180°/4) = cos 120° · tg 45°. Смотрим на косинус: 120° ∈ [90°; 180°] — это II координатная четверть, поэтому cos (2π/3) < 0. Смотрим на тангенс: 45° ∈ [0°; 90°] — это I четверть (самый обычный угол в тригонометрии). Тангенс там положителен, поэтому tg (π/4) > 0. Опять получили произведение, в котором множители разных знаков. Поскольку «минус на плюс дает минус», имеем: cos (2π/3) · tg (π/4) < 0;
6. sin (5π/6) · cos (7π/4) = sin (5 · 180°/6) · cos (7 · 180°/4) = sin 150° · cos 315°. Работаем с синусом: поскольку 150° ∈ [90°; 180°], речь идет о II координатной четверти, где синусы положительны. Следовательно, sin (5π/6) > 0. Аналогично, 315° ∈ [270°; 360°] — это IV координатная четверть, косинусы там положительны. Поэтому cos (7π/4) > 0. Получили произведение двух положительных чисел — такое выражение всегда положительно. Заключаем: sin (5π/6) · cos (7π/4) > 0;
7. tg (3π/4) · cos (5π/3) = tg (3 · 180°/4) · cos (5 · 180°/3) = tg 135° · cos 300°. Но угол 135° ∈ [90°; 180°] — это II четверть, т.е. tg (3π/4) < 0. Аналогично, угол 300° ∈ [270°; 360°] — это IV четверть, т.е. cos (5π/3) > 0. Поскольку «минус на плюс дает знак минус», имеем: tg (3π/4) · cos (5π/3) < 0;
8. ctg (4π/3) · tg (π/6) = ctg (4 · 180°/3) · tg (180°/6) = ctg 240° · tg 30°. Смотрим на аргумент котангенса: 240° ∈ [180°; 270°] — это III координатная четверть, поэтому ctg (4π/3) > 0. Аналогично, для тангенса имеем: 30° ∈ [0; 90°] — это I координатная четверть, т.е. самый простой угол. Поэтому tg (π/6) > 0. Снова получили два положительных выражения — их произведение тоже будет положительным. Поэтому ctg (4π/3) · tg (π/6) > 0.

В заключение рассмотрим несколько более сложных задач. Помимо выяснения знака тригонометрической функции, здесь придется немного посчитать — именно так, как это делается в настоящих задачах B11.

Решение тригонометрических уравнений

В принципе, это почти настоящие задачи, которые действительно встречается в ЕГЭ по математике.

Задача. Найдите sin α, если sin² α = 0,64 и α ∈ [π/2; π].

Поскольку sin² α = 0,64, имеем: sin α = ±0,8. Осталось решить: плюс или минус? По условию, угол α ∈ [π/2; π] — это II координатная четверть, где все синусы положительны. Следовательно, sin α = 0,8 — неопределенность со знаками устранена.

Задача. Найдите cos α, если cos² α = 0,04 и α ∈ [π; 3π/2].

Действуем аналогично, т.е. извлекаем квадратный корень: cos² α = 0,04 ⇒ cos α = ±0,2. По условию, угол α ∈ [π; 3π/2], т.е. речь идет о III координатной четверти. Там все косинусы отрицательны, поэтому cos α = −0,2.

Задача. Найдите sin α, если sin² α = 0,25 и α ∈ [3π/2; 2π].

Имеем: sin² α = 0,25 ⇒ sin α = ±0,5. Снова смотрим на угол: α ∈ [3π/2; 2π] — это IV координатная четверть, в которой, как известно, синус будет отрицательным. Таким образом, заключаем: sin α = −0,5.

Задача. Найдите tg α, если tg² α = 9 и α ∈ [0; π/2].

Все то же самое, только для тангенса. Извлекаем квадратный корень: tg² α = 9 ⇒ tg α = ±3. Но по условию угол α ∈ [0; π/2] — это I координатная четверть. Все тригонометрические функции, в т.ч. тангенс, там положительны, поэтому tg α = 3. Все!

Смотрите также:

1. Радианная и градусная мера угла
2. Тест к уроку «Знаки тригонометрических функций» (1 вариант)
3. Пробный ЕГЭ-2011 по математике, вариант №7
4. Четырехугольная пирамида в задаче C2
5. Задача B2: лекарство и таблетки
6. Задача B4 с таблицами: тарифы на интернет